Regime Finanziario di interesse semplice

Il regime finanziariorappresenta che tipo di regime di interessi viene usato nel calcolo di un montante o di uno sconto.

Definiamo una legge finanziaria ƒ (t) come quella che regola lo scambio di capitali nel tempo.

ƒ (t) può essere riferita a u (t) o v (t), questa funzione dipende da t, cioè dal tempo, bisogna, quindi, fissare una regola di calcolo che ci permette di dire quanto sarà il fattore di montante fra t tempo avendo investito una somma S al tempo 0.

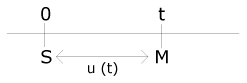
Interesse è uguale al Montante meno la Somma iniziale, cioè:

I = M – S

si può anche scrivere che

I = S ? t

In questo caso ho stabilito una regola generale riguardo agli interessi, ho cioè fissato un Regime Finanziario.

Da questa regola si vede che gli interessi sono proporzionali a S e dipendono dalla durata dell’invetimento (t) e da ?. ? è un termine molto importante perchè, a parità di S e di t, ci dice come varia l’interesse, quindi, ? rappresenta il fattore di proporzionalità.

Il Regime Finanziario è rappresentato dalla formula generale:

i_t = ?t

con u(t) = 1 + i_t.

Guardando al regime finanziario appena definito possiamo dire che:

• gli interessi variano in funzione al tempo;
• siamo in un regime finanziario di interesse semplice.

Immaginiamo un periodo t=1, in questo caso avremo:

i₁ = ? 1

si può dire, quindi, che:

? = i

cioè il tasso periodale di una unità di tempo è uguale ad ?. Da questo ne deriva che:

i_t = i₁ t

in cui i₁ è il tasso annuo di interesse.

Se fissiamo i = 10% si avrà che:

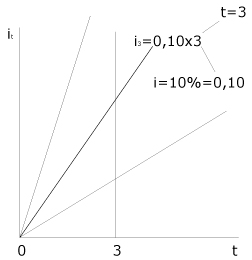
quindi, fissando il valore del tasso di interesse sono in grado di applicare la formula; se avessi i = 0,05 = 5% si avrebbe nel terzo periodo:

i₃ = 0,05 x 3

Il regime finanziario, graficamente, è rappresentato dalle infinite rette sugli assi cartesiani, nel momento che fisso il tasso di interesse vado a scegliere una retta ben precisa.

Per quanto riguarda il contratto finanziario u (t) bisogna:

1. definire il regime finanziario;
2. definire il tasso di interesse i.

Abbiamo già definito il regime finanziario degli interessi semplici:

i_t = i x t

quindi, riamane da definire il tasso di interesse per avere tutti i dati:

u_t = 1 + i_t = 1 + (i x t)

da questa otteniamo il montante nel periodo t:

M = S x u_t = S(1 + it)

per avere l’intensità di interesse:

i_t /t = it / t = i

per l’intensità istantanea d’interesse, invece:

?_t = u’_{(t) / u(t)} = i / (1 + it)

?_t dipende dal tasso di interesse, quindi, ogni interesse ha un’intensità istantanea diversa.

?_t dipende dalla durata, cioè se applichiamo un regime finanziario di interessi semplici, l’intensità istantanea varia al variare del tempo:

se t = 1 => i / (1 + i)

se t = 2 => i / (1 + 2i)

Se ho un capitale C da investire, per la durata t al tasso di interesse annuo i, si avrà:

I = C x i x t

M = C (1 + it)

con 1 + it rappresenta il fattore di montante, graficamente si avrà:

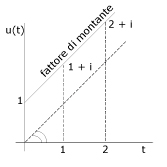
La durata dell’investimento, spesso, è inferiore all’anno, di conseguenza viene espresso in mesi o in giorni, anche in questo caso la formula non cambia:

I = C i (m/12)

I = C i (g/365)

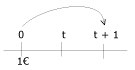
u (t+1) – u (t) = [1 + i (t + 1)] – (1 + it) = i

La particolarità del regime finanziario di interesse semplice è che qualsiasi anno viene osservato, durante il singolo periodo si ha la produzione del tasso di interesse effettivo.

Esempio:

Se ho un finanziamento con un tasso del 5% della durata di 3 anni, allora, so già che ogni anno avrò un tasso di interesse del 5%.

Questa caratteristica del regime finanziario di interesse semplice non si riscontra, invece, nel regime finanziario di interesse composto.

Nel regime finanziario di interesse semplice è presente, quindi, un’ipotesi molto importante:

se ho i=10% e investo 1 nel periodo t=0, allora:
in t=1 avrò un montante pari a 1,10
in t=2 avrò un montante pari a 1 + (0,10×2)
in t=3 avrò un montante pari a 1 + (0,10×3)

cioè, l’ipotesi è che se investo per un anno, per due o per tre, il tasso di interesse é sempre il 10% per ogni periodo; il tasso non cambia con il passare del tempo, si ha: una struttura piatta del piano di interesse (interessi costanti)

Nell’ipotesi che il tasso di interesse vari nei diversi periodi avremo che il cambia la formula generale u(t) = 1 + it, poich´ i tassi nei diversi periodi variano. In questo caso la formula generale diventa:

u(t) = 1 + ?ⁿ _s=1 i_(s) t_(s)

cioé 1 +( i₁ t₁ + i₂ t₂ + … + i_n t_n )