Se ci troviamo in un'epoca x ed investiamo il capitale fino all'epoca y, nel momento in cui arriviamo a y si può decidere di non disinvestire il capitale, ma di lasciarlo fino all'epoca z:

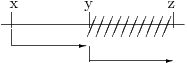
Prendendo una decisione di prolungamento di investimento bisogna chiedersi di quanto crescerà l'ammontare di capitale dall'epoca y all'epoca z.

In altre parole bisogna definire qual è il fattore di montantei di proseguimento.

La cosa da sottolineare è che non dobbiamo trovare il fattore di montante per un'operazione iniziata in y e finita in z, bensì un fattore di montante di un'operazione iniziata in x e proseguita in y fino a z.

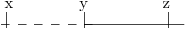
Calcoliamo il rapporto fra il montante per l'impiego iniziato in x e terminato in z e il montante di un investimento iniziato in x e finito in y:

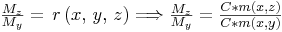
r(x,y,z) rappresenta il fattore di montante di proseguimento, dalla sua formula si vede che m(x,z) e m(x,y) sono due montanti iniziali:

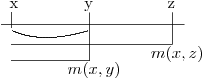
Investo in x il capitale C fino a y, in cui ottengo il montante M_y:

M_y= C * m(x,y)

Se all'epoca x decido di fare un'operazione fino all'epoca z avrò:

M_z= C * m(x,z)

Mz non è un montante di proseguimento, ma un montante iniziale perchè decido in x di investire fino a z.

Per definizione del fattore di montante di proseguimento ho che il montante di proseguimento è:

Mz= M_y * r(x,y,z)

da questa ho:

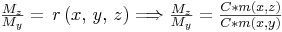
Abbiamo così trovato un'ulteriore formula per fattore di montante di proseguimento.

Il tasso di interessei di proseguimento da y a z, invece, è definito:

r(x,y,z)-1

che può essere riscritto:

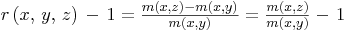
Per avere l'intensità di interesse di proseguimento da y a z (cioè la forza con cui il capitale cresce fra le due epoche):

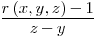
La stessa equazione può essere riscritta in funzione dei fattori di montante:

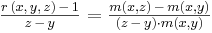
Prendiamo il caso in cui, invece di prolungare un investimento di determinato periodo, si prosegue di un periodo y+u=z variabile. Si può riscrivere la formula nel seguente modo:

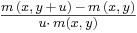
in questo caso stiamo agendo nel continuo, quindi la funzione del fattore di montante può essere scritta mediante .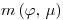

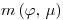
Se , con q=x, è continua e derivabile (derivata parziale rispetto a ) allora esiste il limite destro per .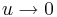

Questo limite lo chiamiamo 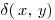la cui formula è la seguente:

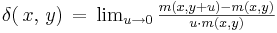
Questa equazione rappresenta l'intensità istantanea di interesse.

L'equazione dell'intensità istantanea di interesse può essere anche scritta come:

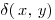= m'_y (x,y) / m (x,y)

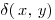
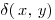sotto il punto di vista finanziario, è un tasso d'interesse riferito ad un istante infinitesimo, invece, che ad un periodo, cioè il tasso di interesse al quale, istante per istante, maturano gli interessi sul montante, fino a quel momento maturato, che vengono immediatamente reinvestiti.

L'intensità istantanea di interesse viene usata per la rappresentazione di fattori di montante, cioè, ogni fattore di montante avrà il suo piccolo ?.