In generale si dice che una Legge finanziaria ( L(x,y) ) è definita se sono definitele due funzioni di capitalizzazione (m(x,y) è il fattore di montante ) e attualizzazione(a(x,y) è il fattore di capitalizzazione):
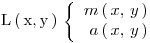

Se il capitale unitario è disponibile in x e l’oprazione termina in y ci dobbiamo attendere m (x, y)>1.
m(x,y) – 1 = Tasso di interesse iniziale (perchè fa riferimento ad un’operazione che inizia in x e finisce in y) per il periodo (x,y).
Se aumenta o diminuisce x o y varierà, di conseguenza, m(x,y).
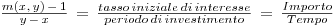
Questa frazione rappresenta l’Intensità di interesse, cioè la forza che ha l’operazione a produrre capitale.
Quando si parla di interesse, quindi, bisogna distinguere fra:
- tasso di interesse: differenza fra montante e capitale iniziale;
- intensità di interesse: rapporto fra tasso di interesse e durata.
Esempio:
Presupponiamo che nel periodo 0,1 siano maturati interessi di 0,07, cioè i0,1= 0,07, avendo investito il mio capitale iniziale, unitario (1€) voglio sapere quanto mi diventerà fra due periodi (cioè due mesi, due anni, etc.), in poche parole voglio sapere quanto sarà il montante unitario.
m (0,1) = 1,07
m (0,2) = 1,144
m (0,3) = 1,225
Quindi, se investo 1000 € avrò che in tre periodi, sempre partendo dal periodo 0:
Un periodo: M = 1000 x 1,07 = 1070 € I = 70 €
Due periodi: M = 1000 x 1,144 = 1144 € I = 144 €
Tre periodi: M = 1000 x 1,225 = 1225 € I = 255 €
Quindi, al crescere della durata dell’investimento, cresce l’interesse in valore nominale.